1. Introduction
It is well known that the high-energy milling process induces high-energy collisions between the raw material and the milling medium, leading to severe plastic deformation, repetitive fracture, and mechanical kneading among the particles of precursor powders [1,2]. Each of these processes has a direct effect on the morphology and the properties of the as-milled products [3]. In this context, it has been reported in the literature that in ductile-ductile systems, the mechanical kneading of particles dominates over the fracture process during milling [1,4,5]. Consequently, as-milled particles tend to agglomerate and, in some cases, they adhere severely to the milling medium and the walls of the vial or container. Consequently, it results, under certain circumstances, in the Ostwald ripening effect, which, in turn, leads to an increase in the size of the as-milled particles [6,7]. For this reason, during the milling of ductile-ductile systems, a balance between mechanical kneading and fracture is not achieved, then the production of nanomaterials, through mechanochemical synthesis, is suppressed.
According to Paul and Pradhan [8], PbTe is a semiconductor material with the potential for various emerging applications due to the control of its properties, which are of special interest. Furthermore, due to its diverse applications, the structural, physical, and chemical properties, among others, of PbTe have been investigated at the atomic level using density functional theory (DFT) investigations [9]. Although experimental results have provided methods and strategies for synthesizing PbTe with various morphological variants [10], theoretical and theoretical-experimental studies have enriched our understanding about the growth mechanisms of PbTe [11,12].
On the other hand, it is important to highlight the role of process control agents (PCAs) during milling; these are primarily organic additives used to regulate the balance between the fracture process and the mechanical kneading during mechanochemical synthesis of nanomaterials [4,13]. Additionally, PCAs control the size of the as-milled particles during milling [14]. It is evident that research opportunities in the field of PbTe formation remain relevant due to the need to understand its growth mechanism in the presence of PCAs. However, theoretical results on how PCAs interact with different surfaces of PbTe, giving rise to its formation, are still lacking. Therefore, targeted approaches in this direction present a landscape of challenges as new research directions. To gain more insights into the PbTe growth mechanism, the aim of this work is to investigate, via DFT, how the PbTe surfaces interact with the process control agent. Through DFT calculations, it is expected to determine, step by step, the sequence of PbTe formation growth. Therefore, one could infer details about the origin of PbTe formation in terms of global and local descriptors obtained via DFT.
2. Computational methods
The effect of formaldehyde (CH2O) as a surface modifier of PbTe is evaluated. To delve into the nature of the CH2OPbTe (surface) interaction, global and local descriptors are calculated using density functional theory. Firstly, the CH2O molecule is structurally optimized in its isolated form. Subsequently, the vertical ionization energy and vertical electron affinity of the CH2O molecule are calculated to elucidate how it behaves energetically in response to electron removal and gain, respectively. Also, the adsorption of the surface modified is studied to elucidate the main components of its interaction with the PbTe surfaces. Then, the results obtained from the electrostatic potential mapped on the van der Waals isosurface, are compared to determine regions with higher and lower charge accumulation. Finally, through Wulff construction, the morphology of the PbTe interacting with CH2O as a process control agent is determined. To obtain the equilibrium morphology of the PbTe, the surface energy is calculated according to the following expression:
where E bar is the total energy of the optimized bar to model the corresponding face, E bulk is the energy of a PbTe formula in the optimized bulk structure, n is the number of PbTe formulas contained in the bar, and S is the corresponding surface area. Details of the bar construction are provided in the following section.
The DFT method chosen was based on the exchangecorrelation functional PBE [15,16]. Additionally, ultrasoft pseudopotentials were used for all atoms, and Grimme’s “D2” dispersion correction, as previously reported in the literature [12]. The Brillouin zone was sampled using a 4×4×1 k-point grid centered at the gamma point, in the case of supercells. On the other hand, the formaldehyde molecule was treated only at the gamma point. The entire method was employed as implemented in the Quantum Espresso 6.1 computing package. Total density-of-states (DOS) as well as projected density-of-states (PDOS) were computed for all the composed systems in their ground state structures. Also, Bader charges were computed for formaldehyde using the code provided by Henkelman’s group [17].
3. Results and discussion
3.1. Formaldehyde effect
Formaldehyde was used as a surface modifier to control the morphology of the PbTe and to suppress the Ostwald ripening effect. Initially, CH2O was structurally optimized, obtaining the structure shown in Fig. 1a). The interatomic distances CH and C-O, calculated at 1.107 and 1.225Å respectively, are in good agreement with the experimentally determined values [18]. The electrostatic potential (ESP) map clearly shows the oxygen atom as the region with the lowest potential, as shown in Fig. 1b). It is consistent with the charge accumulation on the oxygen atom of formaldehyde due to its high electronegativity. Additionally, in the optimized molecule, it was found that the highest occupied molecular orbital (HOMO) is formed by p orbitals in oxygen and sigma bonds in C-H, making the oxygen atom of formaldehyde the most notable site for adsorption on the PbTe surfaces. Besides, the lowest unnocupied molecular orbital (LUMO) is formed by a σ* antibonding orbital in the C=O bond. It is important to mention that frontier molecular orbitals exhibit the most feasible regions of the formaldehyde molecule to react with the lead telluride surfaces [19]. The above since, at first approximation, the HOMO reveals the Fukui function for electrophilic attacks, whereas LUMO is for nucleophilic ones [20]. Thus, electrons can be donated as well as accepted by the oxygen atom in formaldehyde.
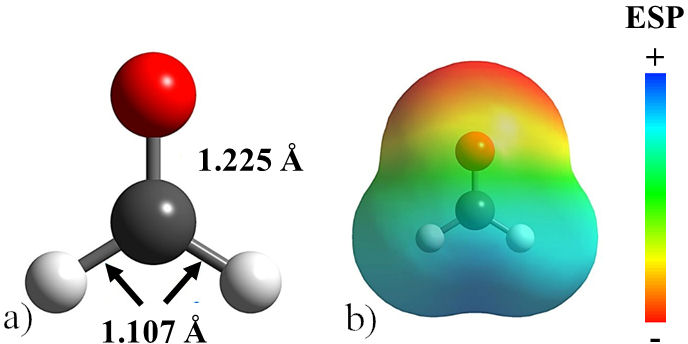
FIGURE 1 a) Optimized structure of the formaldehyde molecule. b) Electrostatic potential map with an isosurface of 0.004 a.u. for the formaldehyde molecule. Relevant bond lengths are indicated.
Global properties of the molecule were also calculated, such as the vertical ionization energy (VIE) and vertical electron affinity (VEA). The obtained values for VIE and VEA were 9.936 and −1.283 eV, respectively. As shown in Fig. 2, another energetic feature was the HOMO-LUMO energy gap, with a value of 3.499 eV. It is important to note that the gap value denotes a kinetically stable molecule. In comparison, a higher energy gap, of about 6.16 eV, was computed at the B3LYP/6-31G(d,p) DFT level by Dwivedi and Shukla [21]. Similarly, a higher HOMO-LUMO gap, calculated as 5.54 eV, was obtained by using the B3LYP functional with empirical basis sets, utilizing d and p polarization functions [22].
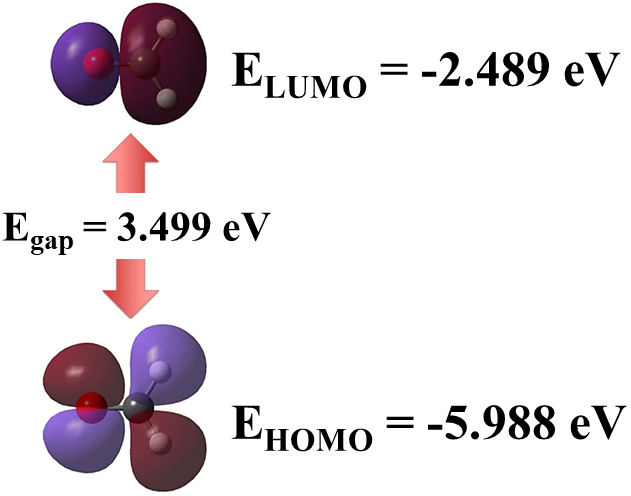
FIGURE 2 Frontier molecular orbitals HOMO and LUMO for formaldehyde molecule. Also, HOMO-LUMO gap is annotated.
In a second step, models of the (100), (110), and (111)Pb surfaces of lead telluride (PbTe) were optimized, as shown in Fig. 3. These plate models were obtained by repeating the PbTe unit cells 3 × 3 × 1 times [23]. The last model exposes only lead atoms on its surface, resulting in vacuum separations between plates of approximately 15Å and distances between periodic repetitions of formaldehyde greater than 10Å. The bottom layer of the plate was fixed to reproduce the atomic coordinates of the crystalline bulk.
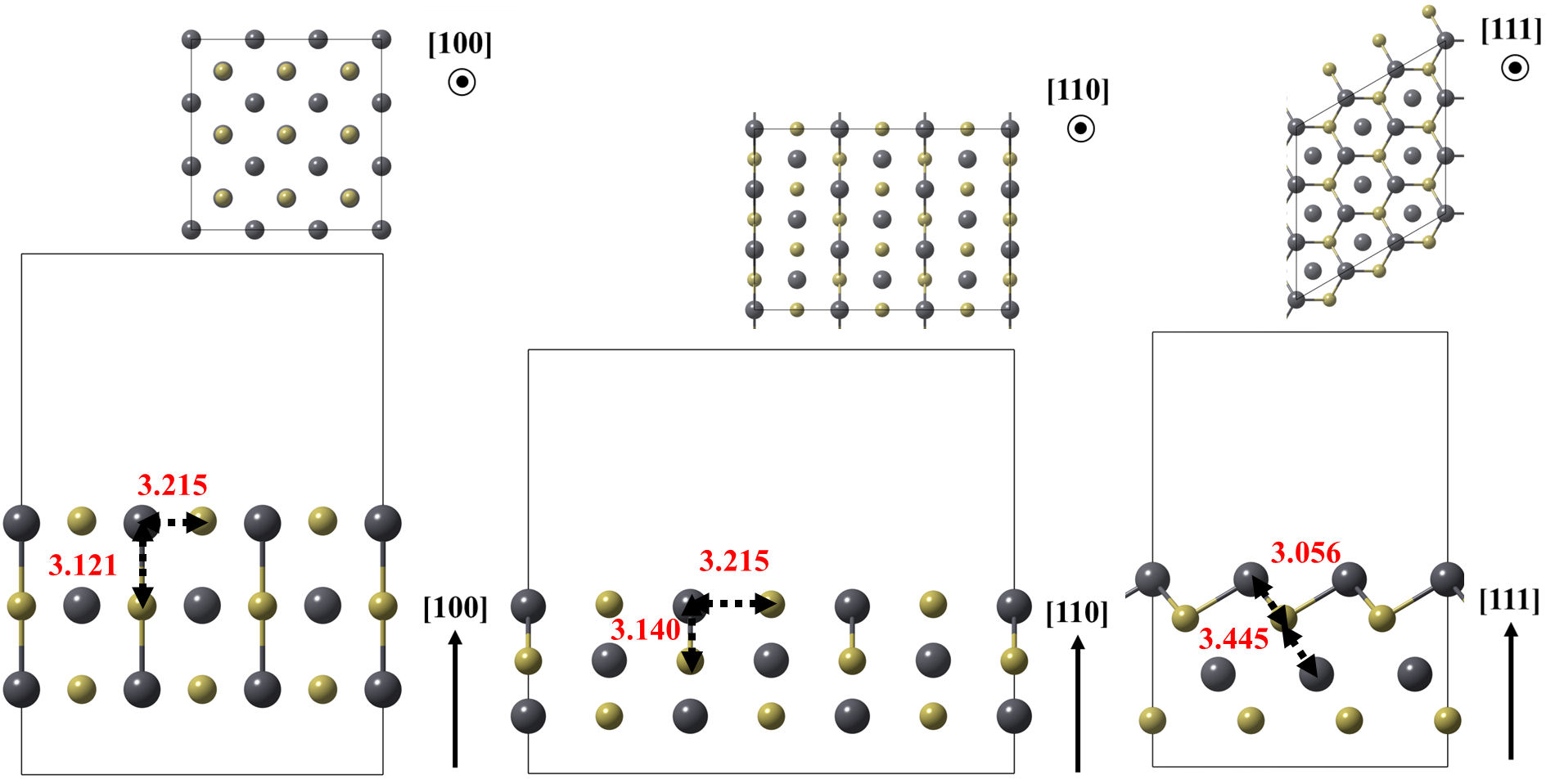
FIGURE 3 Optimized models of the (100), (110) and (111) Pb surfaces of the PbTe. Relevant bonds are annotated in angstrom units. Crystallographic directions are indicated as well.
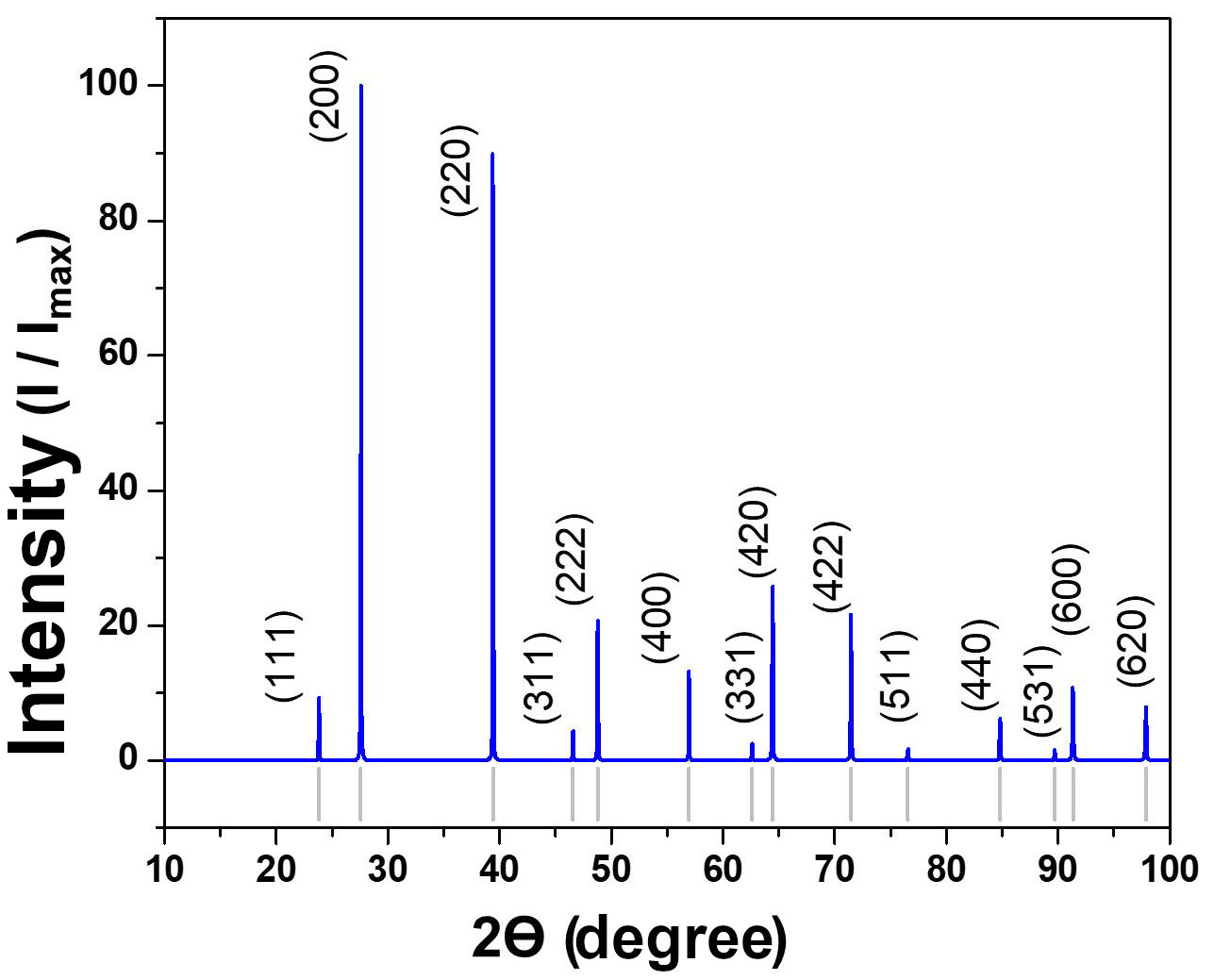
Surface energies, calculated as detailed in the computational methods, indicate an order of γ (100) < γ (110) < γ (111) Pb. Thus, a Wulff model was proposed, where PbTe crystals without a PCA would have a faceted shape. According to the simulated X-ray diffraction pattern (Fig. 4), the faces of higher area and intensity belong to the {100} family. Following this, surfaces with intermediate extent in PbTe crystals will be (110), followed by (111)Pb surfaces.
The interaction with formaldehyde was modeled by allowing the surface modifier to interact with the PbTe plate models. Mostly, the interaction occurred between oxygen and lead atoms. The highest molecule-surface adsorption energy occurred with the (100) surface, in a range from −0.917 to −0.630 eV. Following this, there is a comparable adsorption energy between (100) and (111)Pb surfaces, with maximum values of −0.361 and −0.388 eV, respectively. To analyze the interactions of CH2O with the surfaces under study.
Figures 5 to 7 show the optimized structures for the composed systems in their ground states as well as other lowlying configurations.
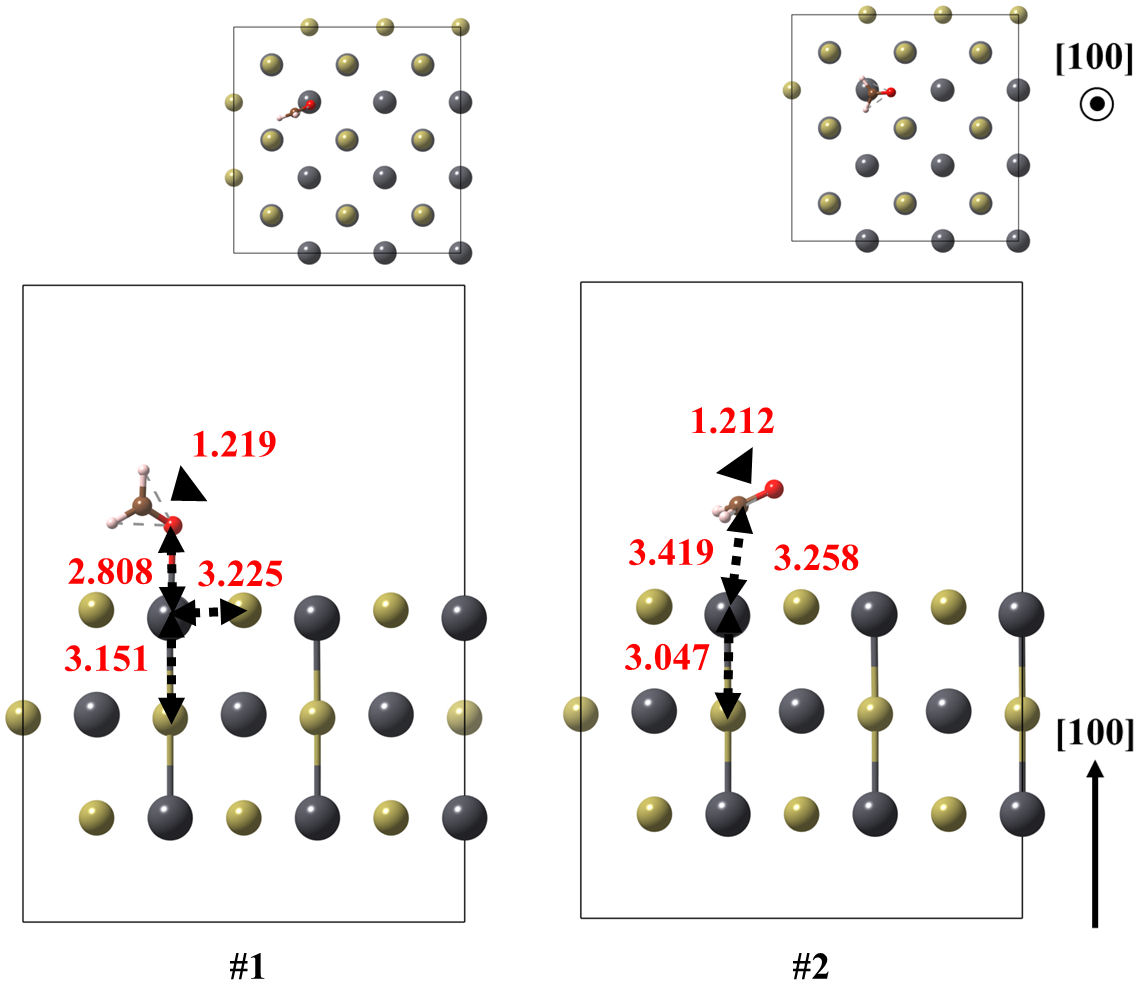
FIGURE 5 Optimized models of the (100) surface of PbTe interacting with formaldehyde, for structures 1 and 2. Relevant bonds are annotated in Å units. Crystallographic directions are indicated as well.
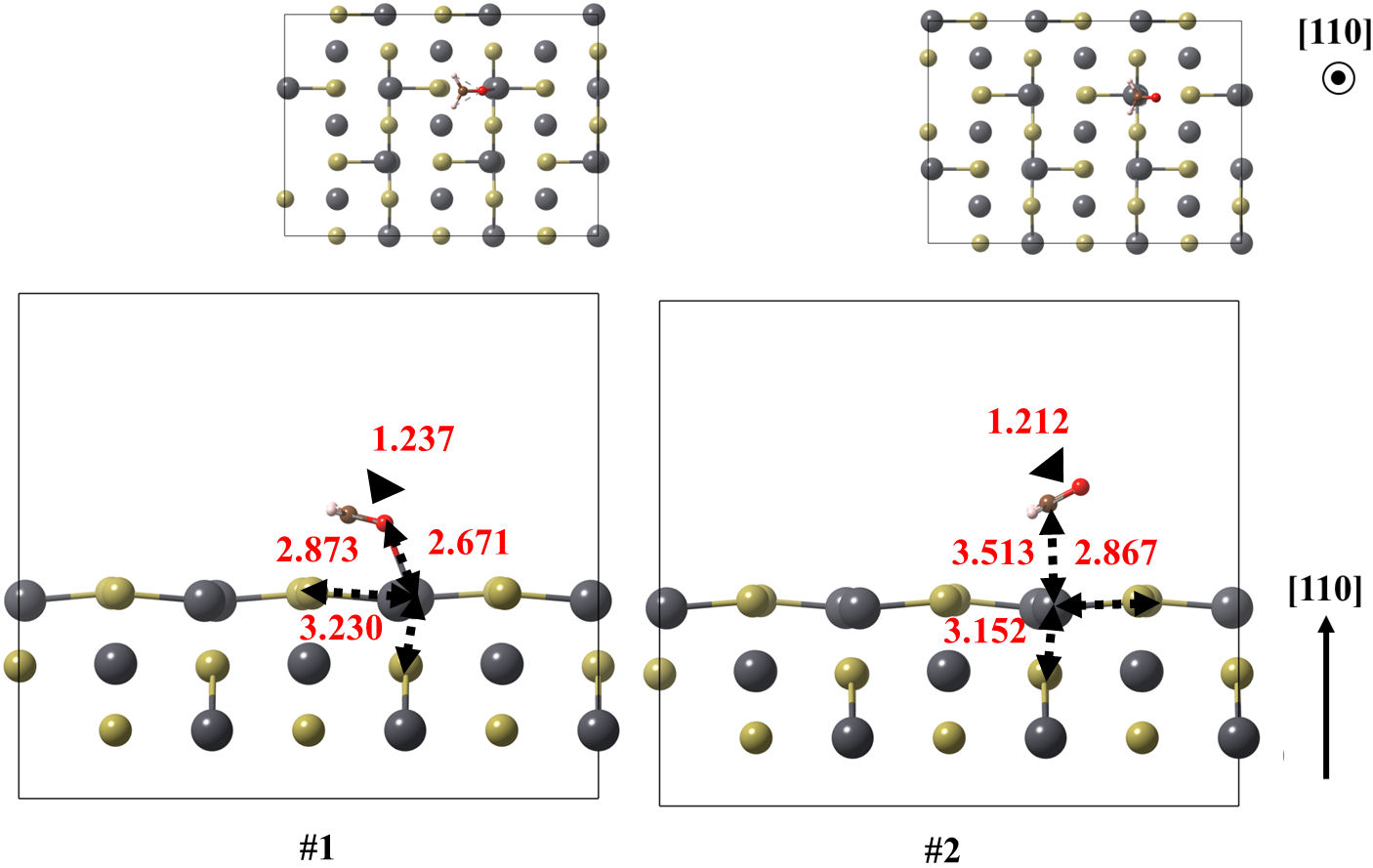
FIGURE 6 Optimized models of the (110) surface of PbTe interacting with formaldehyde, for structures 1 and 2. Relevant bonds are annotated in Å units. Crystallographic directions are indicated as well.
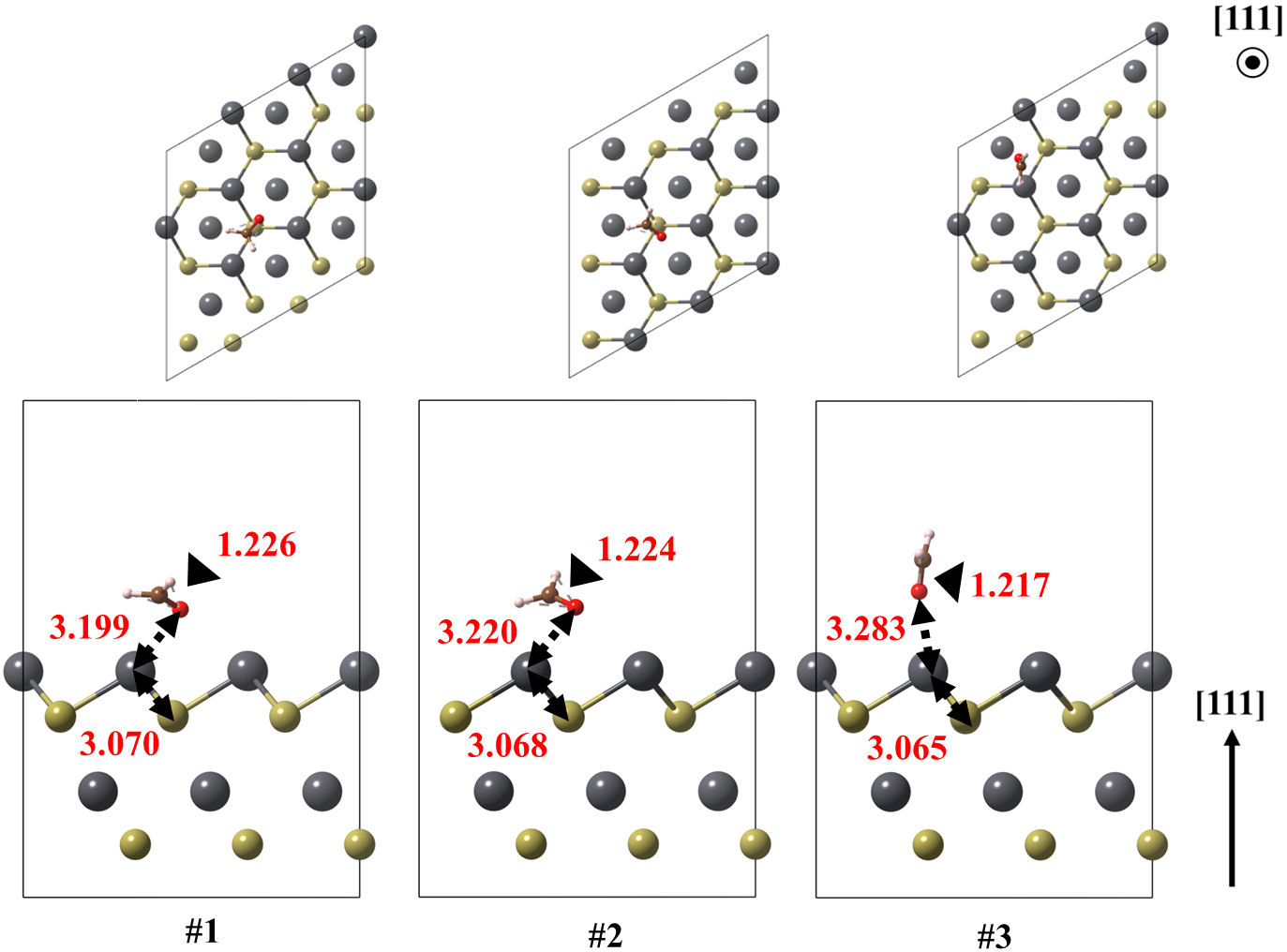
FIGURE 7 Optimized models of the (111) Pb surface of PbTe interacting with formaldehyde, for structures 1 and 2. Relevant bonds are annotated in Å units. Crystallographic directions are indicated as well.
Firstly, the (100) surface with formaldehyde was obtained in two configurations. Whereas the ground state exhibits the CH2O coordinated with the surface by its oxygen atom, with 3.225 Å of bond length and adsorption energy of−0.361 eV, state number 2 is oriented to its carbon atom. That state is 0.172 eV above the ground state and with a lower moleculesurface adsorption energy of about −0.178 eV.
In case of (110) surface, the ground state and the following low-lying structure are obtained with 0.288 eV of energy difference. Once again, the ground state structure is obtained with the (CH2O) attached to the surface by oxygen, whereas the other is state by carbon. In these case, the shortest molecule-surface bond lengths are reduced down to 2.671 and 2.867 Å respectively. In this case, the adsorption energy is −0.917 eV.
The lead-terminated (111)Pb surface obtained three different feasible structures, all of them oriented to the oxygen atom of CH2O. In addition, the large Pb-O bond lengths, above 3 Å, and the −0.388 eV of adsorption energy suggest an electrostatic interaction. All the Pb-O bond lengths for the ground state structures are found ranging from 2.671 to 3.199 Å. These values are larger than those obtained in the case of PbO, of about 2.3 Å.
3.2. Theoretical approach to PbTe morphology
In all cases, the electrostatic potential maps showed that the interacting formaldehyde molecule, in its ground state, is directed to the lead atom by its region with low ESP. The above is consistent with the highest electronegativity of oxygen in comparison to all the constituents for formaldehyde (Fig. 8). Interactions between the CH2O and the surface are mostly polar-electrostatic, as charge donations took place. In addition, the calculation of the total Bader charge on the surface modifier molecule exhibited that formaldehyde received a charge from the lead telluride surface, ranging from −0.045 to −0.152 e. Although this charge transference is scarce, the above can be related to the notable coordination of formaldehyde on the surface, attributed to a mixed chemysorption-physisorption of the molecule. To state the relationship between the orbitals of the interacting moieties, the total density-of-states for all the interacting systems as well as the projected density-of-states are analyzed below.
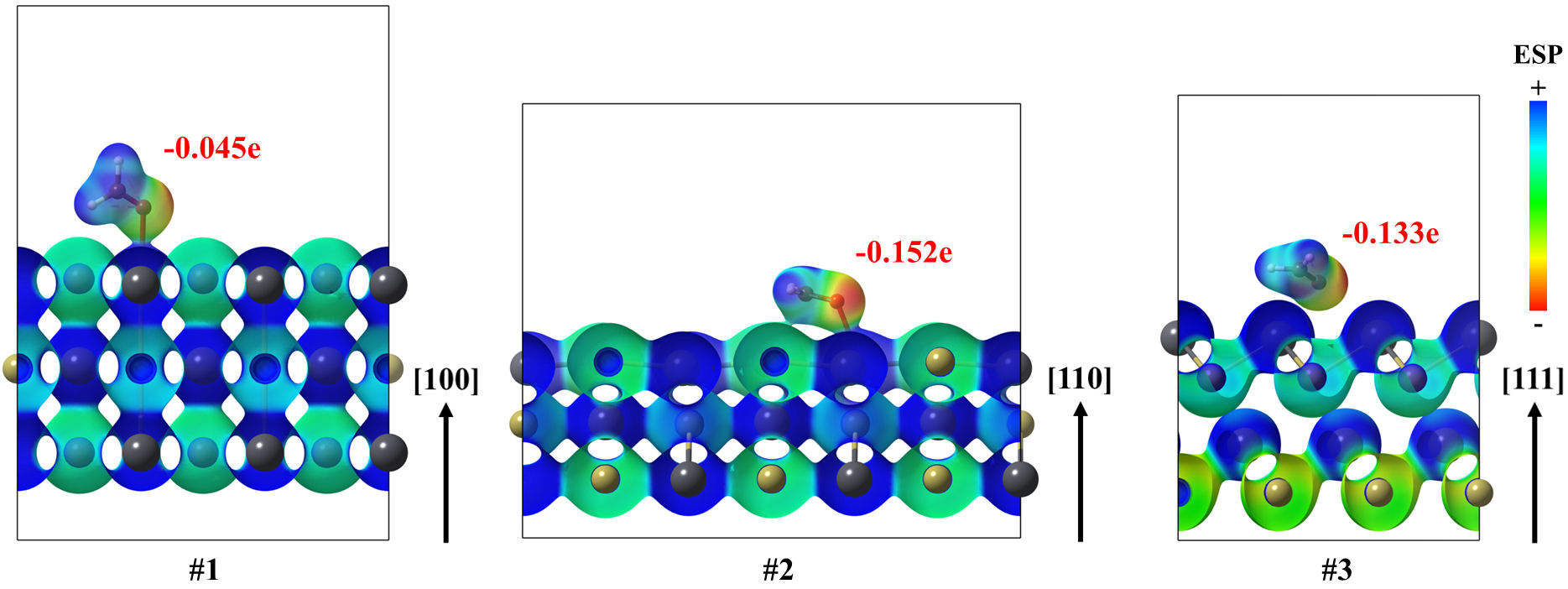
FIGURE 8 Electrostatic potential mapped on isosurfaces, with 0.02 a.u. of electron density, for (100), (110) and (111) Pb surfaces of the PbTe interacting with formaldehyde in their ground states. Also, Bader charges on formaldehyde are annotated as well.
To elucidate the shape of the electronic structure of the systems under study, Fig. 9 shows their DOS/PDOS near the Fermi level. All the surfaces are obtained with the 2p orbital of the oxygen atom of formaldehyde with an important overlap with those from the Pb, explaining the chemical part of their interaction. C (2p) orbital of CH2O is also available to be overlapped with those from surface lead atoms. Although the DOS/PDOS of the slabs models provide only partial information for the surfaces under study, it is noticeable that those for (100) and (110) surfaces qualitatively reproduce the result of bulk PbTe [24,25]. According to calculations performed by Aguado-Puente and colleagues, at GW method as well as within DFT with the PBE functional, the PbTe is a semiconductor with a narrow bandgap of about 0.2 to 0.4 eV [26] at the L point. The above is in full agreement with the experimental result of 0.190 eV, measured at 4 K of temperature by absorption luminescence, reported by Zasavistskii and coworkers [27]. However, the slab models obtained important deviations, with values ranging from 0.0 to 0.744 eV.
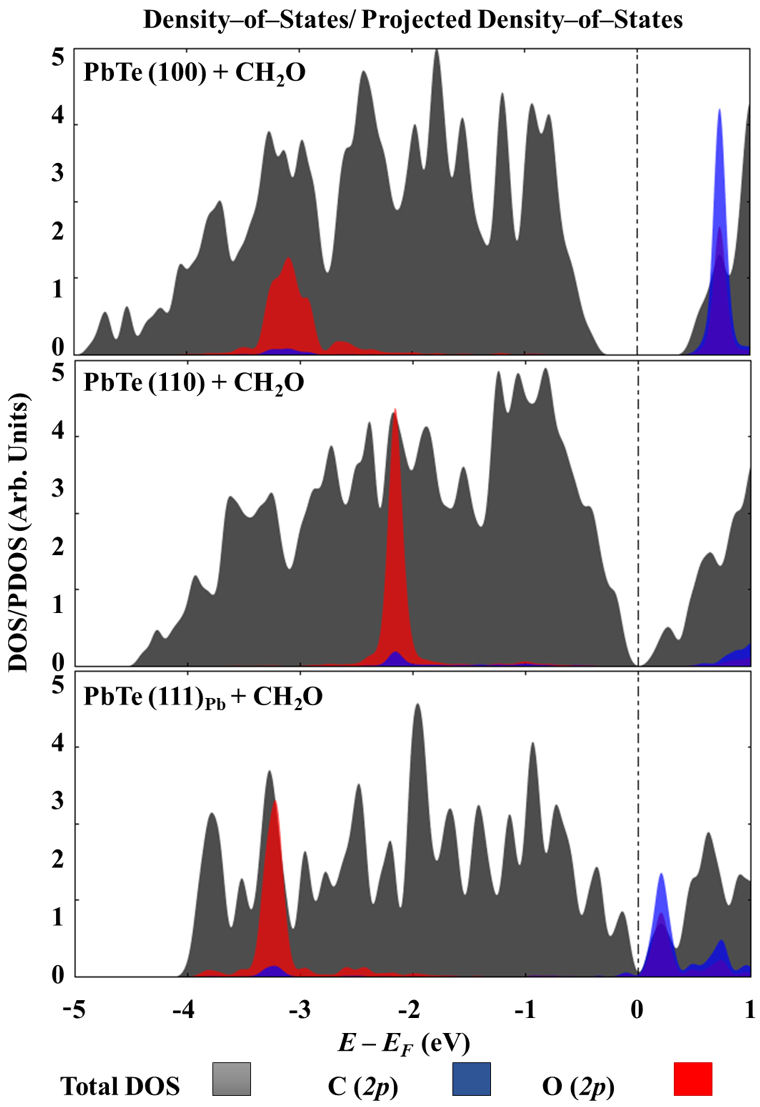
FIGURE 9 Total density-of-states for all the interacting systems as well as projected density-of-states in case of C (2p) and O (2p) orbitals on formaldehyde.
The adsorption of the CH2O molecule also modifies the surface energy of the PbTe. The greatest change in surface energy was found for the (110) surfaces, calculated at ∆γ = −3.49 meV Å−2. Following this, the increase on the (110) surfaces is −2.79 meVÅ−2, while for the (100) surface, is only −1.94 meVÅ−2. Thus, formaldehyde stabilizes the (110) and (111)Pb facets, making them energetically more favorable to be expressed on the surface of the PbTe crystals.
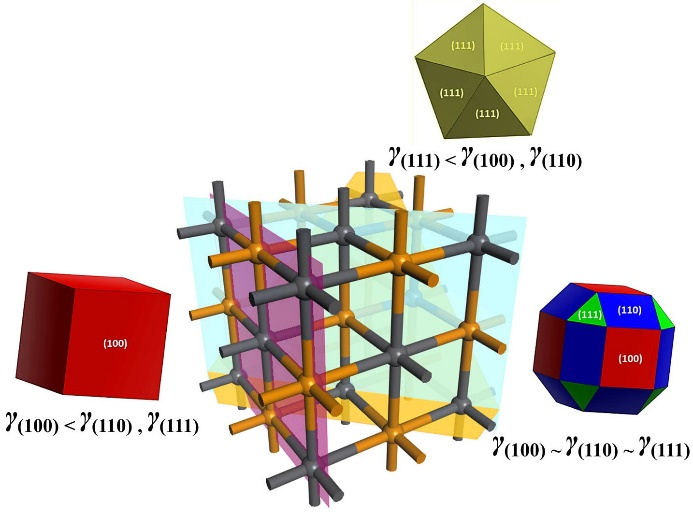
Following the Wulff construction, the PbTe crystals can be obtained with different morphologies. For example, starting from a situation without using a surface modifier (ACP), with surface energies in the order γ (100) < γ (110) < γ (111)Pb , PbTe crystals should mostly exhibit cubic shapes. However, by adding the surface modifier, the stabilization of the (110) and (111)Pb faces leads to a situation where the energies follow the order γ (100) ≈ γ (110) < γ (111)Pb , resulting in faceted and rounded PbTe crystals. Another possibility is that the surface modifier produces an energetic situation in which γ (100) ≈ γ (110) ≈ γ (111)Pb . Thus, PbTe crystals will be mostly rounded, displaying all three facets. Finally, as shown in Fig. 10, a last possibility is that the most favored facet is the {111} family, where the coalescence of tetrahedra leads to a decahedral geometry in an energetic situation γ(111) < γ(110),γ(100).
The aforementioned possibilities are dependent on the size of the PbTe crystals, without the Wulff model having sufficient scope to provide a clear relationship between surface energies and geometry based on crystal size. However, evidence of the existence of the described forms has been reported in the literature [12], indirectly supported by the highintensity peaks in the simulated X-ray diffraction pattern in Fig. 4.
4. Conclusions
Through DFT calculations, it was understood that the growth of quasi-cubic PbTe relies on geometric and energetic constraints. The change in the energetic situation of the exposed facets can be attributed to surface modifiers, such as formaldehyde in this study. While surface energies follow the order γ (100) < γ (110) < γ (111)Pb for the system without a surface modifier, this order can be altered due to the stabilization produced by the formaldehyde molecule. Additionally, it was observed that obtaining decahedra and faceted morphologies of PbTe is possible.
According to the calculations performed within DFT, these morphologies are due to comparable surface energies γ, with Wulff shapes exhibiting the (100) and (111) faces. Furthermore, the modified decahedron Wulff shape results from the stabilization of the (111) faces, while the faceted Wulff shape is obtained because the (100), (110), and (111) faces are energetically competitive. While the Wulff construction does not predict the shape of particles based on their size, it does provide insight into the reasons they exhibit the morphologies observed experimentally.










 nueva página del texto (beta)
nueva página del texto (beta)